¿Por qué el aprendizaje competencial en matemáticas es el camino a seguir?
Ver las referencias bibliográficas
En numerosas ocasiones me han preguntado por qué creo firmemente en el aprendizaje competencial en matemáticas y por qué lo considero la vía más efectiva. Exploremos detalladamente las diferencias entre el aprendizaje competencial y el no competencial, además de diferentes ejemplos que destacan las ventajas de uno sobre el otro. Así que, ¡vamos con ello!
Para empezar, el aprendizaje competencial fomenta el desarrollo de habilidades y competencias clave, más allá de la retención y memorización de los contenidos. Es fundamental poder llevar a cabo este enfoque en el aula de matemáticas porque nos ayuda a potenciar la deducción, la argumentación y el pensamiento crítico en nuestros alumnos, habilidades esenciales para el día de mañana.
Por ejemplo, imagina que estás aprendiendo a cocinar. Si has aprendido competencialmente a hacer un pastel, en lugar de limitarte a seguir recetas punto por punto, comprenderás por qué ciertos ingredientes combinan bien, como los diferentes métodos de cocción afectan el sabor y la textura, y cómo adaptar las recetas según los ingredientes disponibles en casa. Así, cuando nos encontramos con situaciones como: "¡Me falta levadura para hacer el pastel!", somos capaces de resolver el problema sustituyendo la levadura por bicarbonato combinado con una sustancia ácida como el zumo de limón, u otro ingrediente que tenga propiedades similares para hacer que la masa del pastel se eleve adecuadamente.
En realidad, el aprendizaje competencial nos prepara no solo con hechos y datos, sino que nos ayuda a desarrollar la capacidad de pensar críticamente, resolver problemas y aplicar lo que hemos aprendido en nuevos contextos.
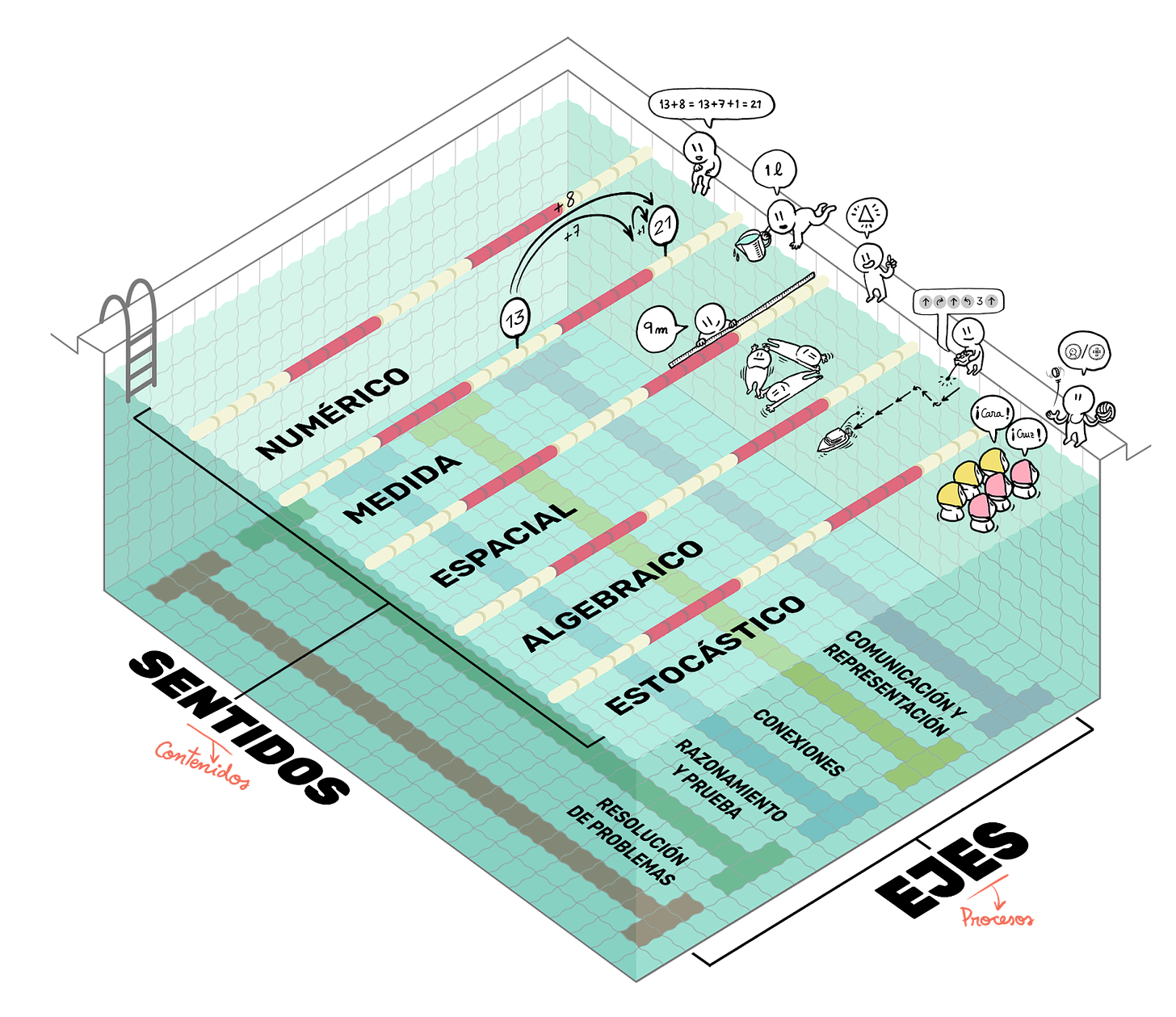
La piscina del aprendizaje competencial
Esta piscina es un poco inusual, las líneas de los carriles no coinciden con las del suelo. Dentro de las matemáticas tenemos contenidos de diversos bloques: sentido numérico, de la medida, espacial, algebraico y estocástico. Esto es relevante en todas las etapas educativas. Por ejemplo, durante mucho tiempo se pensaba que el álgebra solo debía enseñarse en secundaria, pero se ha visto que es importante trabajar todos estos bloques desde primaria.
En el fondo de esta piscina están los procesos matemáticos. Ser un buen matemático implica no solo conocer los contenidos, sino también ser un resolutor de problemas eficiente, saber razonar, saber hacer conexiones entre diferentes bloques de contenido y en otros ámbitos y trabajar muy bien la comunicación y representación. Esto es lo que hace que un alumno sea completo en matemáticas.
El hecho de que los carriles estén girados es significativo porque no queremos alumnos que solo se destaquen en un área, sino alumnos integrales que dominen todos los aspectos matemáticos.
El alumno competente en matemáticas debe moverse como pez en el agua, cambiando de carril, buceando y que sepa ir a la superficie cuando es necesario. La piscina, para funcionar, necesita estar llena de agua, y en este caso, el agua representa la capa socioemocional. Esta es indispensable para el aprendizaje. Si los alumnos tienen bloqueos o ansiedad matemática, debemos gestionar el aula de manera que puedan fluir y aprender sin barreras.
La clave en el aula
Para implementar el aprendizaje competencial en las aulas, debemos verlo como un todo integrado. Las actividades en clase deben cubrir tanto los contenidos como los procesos a la vez. Esto garantiza que los alumnos puedan construir conocimiento manera efectiva y significativa.
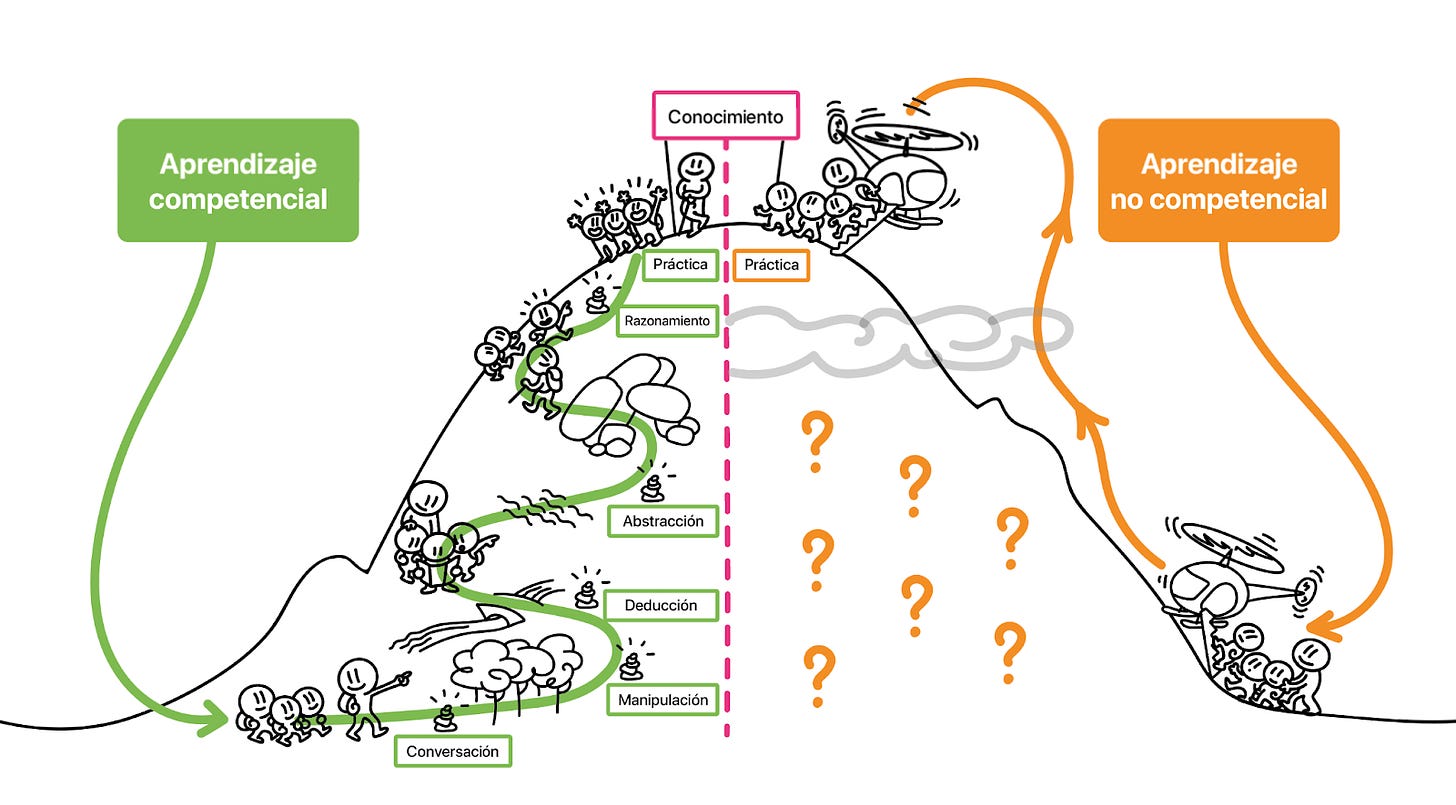
¿Llegamos al mismo punto fomentando el aprendizaje competencial?
Imagina la trayectoria del aprendizaje competencial de un contenido concreto como ascender una montaña. Cada paso es una oportunidad para trabajar en procesos y construir activamente el conocimiento. Conocer el camino hacia la cima no solo te permite retroceder si es necesario reconstruir un concepto, sino que también te dará las herramientas para enfrentar situaciones similares en el futuro.
Descárgate el infográfico en castellano
Descarrega l’infogràfic en català
Descarga el infográfico para compartir con tus compañeros por qué aprender matemáticas de manera competencial es el camino.
Con el aprendizaje basado en competencias, los alumnos aprenden subiendo la montaña paso a paso, disfrutando de un camino que, quizás es más largo, pero es más enriquecedor. A través de la conversación, la manipulación, la deducción, la abstracción y el razonamiento, los alumnos descubren y dominan los procesos matemáticos. De este modo, al final del camino, para consolidar el conocimiento que queremos construir, deben practicar lo aprendido, asegurando también una automatización de los contenidos matemáticos.
Siguiendo con la metáfora de la montaña, esto contrasta con la rápida pero menos significativa y gratificante experiencia de ser llevado en helicóptero directamente a la cima. En este enfoque no competencial, se explica directamente a los alumnos los contenidos y se les pide que practiquen. Sin embargo, no les damos las herramientas para que puedan consolidar los conocimientos y hacer conexiones que les ayuden a entrelazar significativamente el contenido que queremos construir.
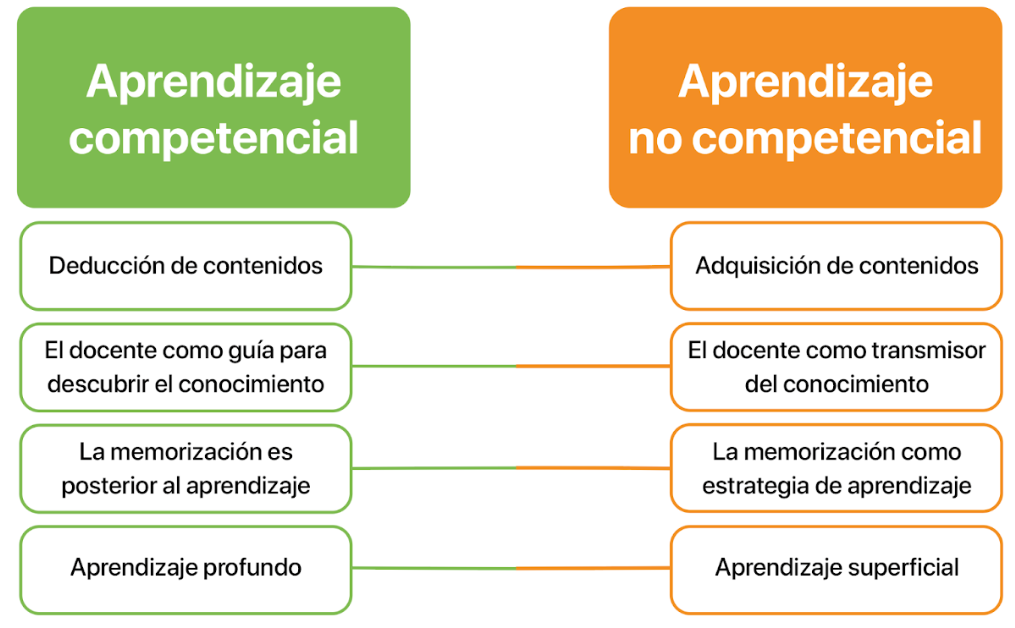
Los aprendizajes no son los mismos
En el marco del aprendizaje competencial, construimos el conocimiento a través de la deducción y la práctica en el aula. El docente asume el papel de guía, convirtiéndose en el facilitador del camino hacia el conocimiento, donde los alumnos descubren y conectan los conceptos. En este sentido, es esencial que los docentes sepamos hacer las preguntas indicadas para acompañar a los alumnos a desarrollar deducciones, argumentos y conclusiones.
Por lo contrario, en el aprendizaje no competencial, el docente es el principal transmisor de conocimiento, sin fomentar que el alumno lo desarrolle por sí mismo. Este segundo enfoque puede resultar en una comprensión más superficial del contenido, donde la memorización suele ser la principal —y a veces la única— estrategia de aprendizaje.
La memorización debe ser posterior al aprendizaje, no la estrategia para aprender
En el aprendizaje competencial, la memorización no es el punto de partida, sino el resultado natural de un aprendizaje profundo. Solo después de entender y aplicar los conceptos, los alumnos consolidan su conocimiento a través de la práctica y la memorización, asegurando una retención duradera de los contenidos.
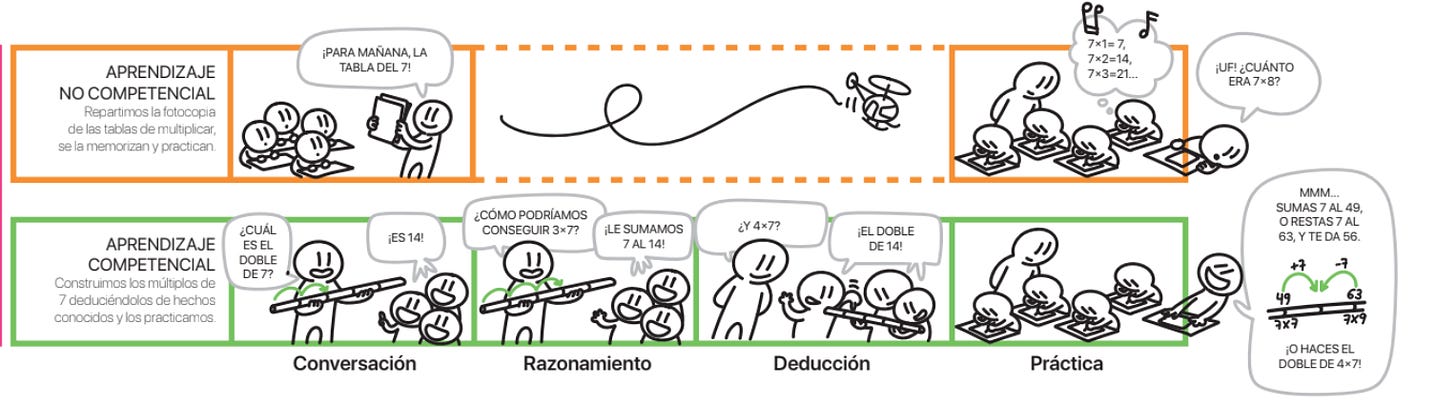
¡Veámoslo con un ejemplo! La tabla del 7
En esta ilustración, en el caso del aprendizaje no competencial, vemos un aula donde el docente reparte fotocopias de la tabla del 7 (en este caso dar la fotocopia representaría haberlos subido en helicóptero) y se les da la siguiente instrucción:
“¡Para mañana, la tabla del 7!”
Los alumnos memorizan la tabla del 7 sin comprender de dónde sale cada resultado. “4x7=28 porque lo dice la fotocopia”. Su aprendizaje se basa en repetir y repetir sin pensar. De hecho, a veces inventan una cantinela que les ayuda. De este modo aprenden las tablas de multiplicar de manera mecanizada y memorística. Al día siguiente, practican recordando:
“7x1=7, 7x2=14, 7x3=21…”
En cambio, en el enfoque competencial, el aula se transforma en un espacio de descubrimiento. Aquí, el docente guía a los alumnos a construir los múltiplos del 7 mediante la conversación, el razonamiento y la deducción. Los alumnos descubren que existe un abanico de estrategias para dar con los resultados de muchas multiplicaciones.
"¿Cuál es el doble de 7?" - Pregunta el docente.
Y los alumnos responden con entusiasmo:
"¡Es 14!".
A través de la conversación y la manipulación, descubren como sumar 7 al 14 para encontrar el siguiente múltiplo, participando activamente en su aprendizaje. Y cuando el profesor pregunta:
“¿Y 4x7?”
Los alumnos responden:
“¡El doble de 14!”
“¡O le sumamos 7 a 3x7!”
“¡O le restamos 7 a 5x7!”
Mientras tanto, algunos alumnos que aprenden de manera no competencial pueden tener dificultades para realizar multiplicaciones más difíciles si no recuerdan los resultados que memorizaron:
“¡Uf! ¿Cuánto era 7x8? - pregunta el alumno.
Vemos que los alumnos de la viñeta del aprendizaje competencial son capaces de construir los múltiplos de 7 deduciéndolos de hechos conocidos. Han aprendido diferentes estrategias para saber multiplicar, y eligen las que mejor les funcionan:
“Mmm… Si sumamos 7 al 49, o restamos 7 al 63, obtenemos 56. ¡O simplemente duplicamos 4x7!” - razona el otro alumno.
Solo cuando ya se han construido los conocimientos, se pasa a su práctica y sistematización. Aquí el docente actúa como guía esencial en la construcción del conocimiento matemático, guiando el aprendizaje de los alumnos a través de las preguntas adecuadas.
El aprendizaje competencial es el camino a seguir
El aprendizaje competencial no solo construye una base sólida en matemáticas, sino que también desarrolla habilidades esenciales para la vida. Al permitir que los alumnos exploren, descubran y deduzcan, fomentamos un aprendizaje profundo y duradero que va más allá de las matemáticas.
Referencias bibliográficas
A continuación, os dejo las referencias bibliográficas con las que he construido el infográfico sobre el aprendizaje competencial.
Os selecciono la bibliografía más relevante que pone en valor los procesos matemáticos a demás de los contenidos.
Resolución de problemas:
Schoenfeld, A. H. (2007). Problem solving in the United States, 1970–2008: Research and theory, practice and politics. ZDM, 39(5), 537-551. https://doi.org/10.1007/s11858-007-0038-z
Pólya, G. (1945). How to solve it: A new aspect of mathematical method. Princeton University Press.
Razonamiento y prueba:
Simon, M. A., & Blume, G. W. (1996). Justification in the mathematics classroom: A study of prospective elementary teachers. The Journal of Mathematical Behavior, 15(1), 3-31. https://doi.org/10.1016/S0732-3123(96)90036-X
Pólya, G. (1968). Mathematics and plausible reasoning. Princeton University Press.
Conexiones y modelización:
Maaß, K. (2006). What are modeling competencies? ZDM, 38, 113-142. https://doi.org/10.1007/BF02655885
De Lange, J. (1989). Trends and Barriers to Applications and Modelling in Mathematics Curricula. In W. Blum, M. Niss, I. Huntley (Eds.), Modelling, applications and applied problem solving (pp.196-204). Chichester: Ellis Horwood.
Comunicación y representación:
Mainali, B. (2021). Representation in Teaching and Learning Mathematics. International Journal of Education in Mathematics, Science and Technology, 9(1), 1-21.
Greeno, J.G., & Hall, R.P. (1997). Practicing representation: Learning with and without representational forms. Phi Delta Kappan, 78, 361-367.
Las siguientes referencias plantean que las matemáticas competenciales deben potenciar los procesos anteriormente citados, sin renunciar a los contenidos. Esta bibliografía forma parte del marco teórico reconocido internacionalmente por entidades (OCDE, NCTM) y curriculums.
National Council of Teachers of Mathematics (2000). Principles and Standards for School Mathematics.
Niss, M., & Højgaard, T. (2019). Mathematical competencies revisited. Educational Studies in Mathematics, 102(1), 9-28.
Hiebert, J., & Wearne, D. (2003). Developing understanding through problem solving. In Schoen, H. L., & Charles, R. I. (Eds.), Teaching mathematics through problem solving: Grades (pp. 6–12). Reston, VA: NCTM.
NCTM (2014, April 18). Access and Equity in Mathematics Education. A position of the National Council of Teachers of Mathematics.
A continuación os selecciono bibliografía sobre el rol del docente cómo facilitador del descubrimiento guiado y la estructuración de contenidos:
Ruiz Martín, H. (2023). “Edumitos”: ideas sobre el aprendizaje sin respaldo científico. Internacional Science Teaching Foundation. Capítulo 3: “Las personas aprenden mejor cuando descubren las cosas por su cuenta”.
Banchi, H. & Bell, R. (2008). The many levels of inquiry. Science and children, 46(2), 26.
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4–14. https://doi.org/10.3102/0013189x015002004
Este libro es fundamental sobre trayectoria didáctica de numeración y cálculo y construcción del conocimiento. Ayuda a entender que la memorización no debe ser la estrategia de aprendizaje, sino el resultado.
Van Den Heuvel-Panhuzien, M. (2008). Children Learn Mathematics. A Learning-Teaching Trajectory with Intermediate Attainment Targets for Calculation with Whole Numbers in Primary School. Dutch Design in Mathematics Education, V: 1. Utrecht. Freudenthal Institute
En este bloque de referencias se puede entender qué significa aprendizaje profundo y aprendizaje superficial.
Ausubel, D.P. (2012). The Acquisition and Retention of Knowledge: A Cognitive View. Science & Business Media.
Hiebert, J., & Wearne, D. (2003). Developing understanding through problem solving. In Schoen, H. L. & Charles, R. I. (Eds.), Teaching mathematics through problem solving (pp. 6–12). Reston, VA: NCTM.
Schoenfeld, A. (1992). Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics. A Grouws D. A. (Ed.), Handbook for Research on Mathematics Teaching and Learning. Macmillan Publishing Company.
Dewey, J. (1933). How we think. Boston: Heath.