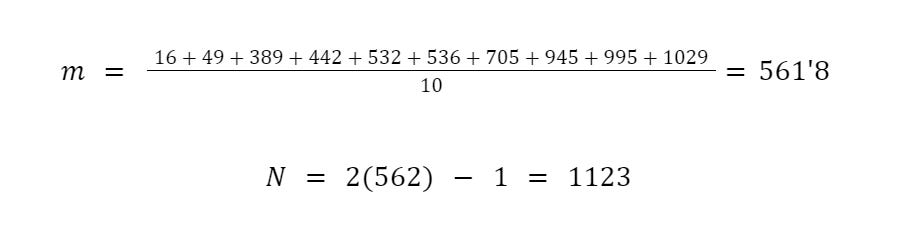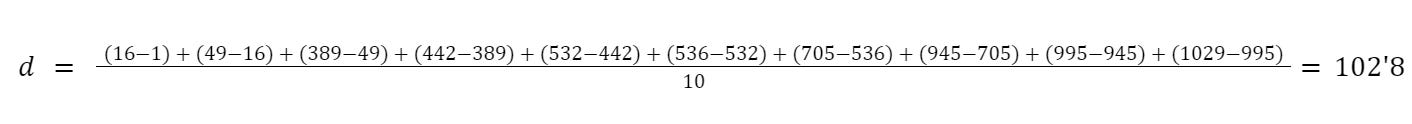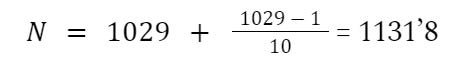El problema de los tanques alemanes | Mi comunicación en las JAEM21 (Jornadas del Aprendizaje y la Enseñanza de las Matemáticas 2024)
Reflexionando sobre los conceptos de estimación, aproximación y variabilidad a partir de la gestión de aula de un problema de estadística y probabilidad para secundaria
Ser docente de matemáticas es una profesión preciosa. Se trata de compartir, de hacer aprender y de reaprender. De gestionar una clase, de observar a los compañeros, de formarse continuamente.
Por esta razón, cada dos años tenemos una cita imprescindible: las JAEM (Jornadas del Aprendizaje y la Enseñanza de las Matemáticas). En esta vigesimoprimera edición en Santander hemos vivido cuatro días de jornadas intensísimas, con muchas comunicaciones y talleres de primer nivel y centenares de docentes con los que conectar y compartir ideas. ¡Gracias a todos por esta experiencia!
Este año, presenté un taller de estadística y probabilidad para secundaria. Hoy os traigo la charla en formato escrito, un problema para hacer muchas conexiones ideal para trabajar la estimación, la aproximación y la variabilidad estadística.
El problema de los tanques alemanes
En gran grupo, presentamos «El problema de los tanques alemanes», extraído del artículo de Xavier Bardina, Sílvia Prior, Carla Rodríguez y Ferran Rosado, del Departamento de Matemáticas de la Universidad Autónoma de Barcelona.
La Segunda Guerra Mundial forma parte de nuestra historia reciente, pero lo que no es tan conocido es que detrás de todos aquellos hechos históricos la estadística también jugó un papel importante.
[...] La información sobre la industria y las plantas de producción alemanas eran datos esenciales para diseñar el programa de bombardeos estratégicos sobre el continente europeo. Este problema de estimación de la producción militar alemana en el mundo anglosajón, y en el mundo de la estadística en general, es conocido como el problema de los tanques alemanes.
Para resolverlo, el departamento de inteligencia de las fuerzas Aliadas utilizó de entrada las técnicas habituales de espionaje, como son descodificar mensajes encriptados, interrogatorios... que daban unas estimaciones muy elevadas y muy alejadas de la producción real. Así pues, decidieron que era el momento de buscar alternativas que dieran unas cifras más reales para poder trabajar y preparar sus estrategias militares. En ese momento es cuando intervino el ingenio de los estadísticos con la ayuda inconsciente de los alemanes. [...]
Cada una de las clases de carruajes de la Wehrmacht llevaba un tipo de caja de cambios que había sido numerada de forma correlativa. Así pues, existía una relación entre cada serie de caja de cambios y el tipo de carruaje. Por lo tanto, si se pudiera determinar la producción de una serie completa de cajas de cambio, se obtendría la producción de los tanques Panzer asociados. Entonces, con unos cuantos tanques capturados a los alemanes y con la ayuda de los estadísticos se podría estimar su producción de carruajes de combate.
Después de la guerra, se conocieron los datos reales y se vio que las estimaciones matemáticas habían sido muy certeras mientras que los resultados de la inteligencia distaban mucho de la realidad. [...]
La tabla que viene a continuación [...] refleja en números la precisión de las estimaciones llevadas a cabo por los estadísticos y permite comprobar la gran diferencia con las que realizó en un primer momento la inteligencia de los aliados.
Con el grupo, iniciaríamos un debate sobre cómo creen que el ejército aliado utilizó la estadística para estimar la cantidad de tanques alemanes.
¿Cómo lo haríamos nosotros en clase? Estimemos la cantidad de papelitos numerados que hay en una bolsa
Mostraremos a los alumnos una bolsa llena de papelitos numerados, tantos como tanques. Será nuestro conjunto a estimar.
Dejaremos un tiempo para que, individualmente, hagan una estimación de la cantidad de papelitos que hay. De esta manera, tendremos muchas estimaciones.
A partir de la gestión de aula, podemos guiar la conversación para establecer un intervalo razonable de las estimaciones de los alumnos. Como la diferencia entre los dos valores, seguramente, será muy grande, sugeriremos que necesitamos más información para poder hacer una estimación más acertada. ¿Nos ayudará la estadística a ello?
Planteamos estimadores sobre el tamaño de la población numerada
Queremos estimar el tamaño de una población numerada 1, 2, 3,…, N. Si sacamos una muestra de 10 papelitos, ¿qué podríamos decir sobre la cantidad total?
Tendríamos una muestra aleatoria simple sin reposición de medida n.
¡Hagamos el experimento! Saco 10 papelitos al azar.
En este ejemplo, al menos ya vemos que habrá como mínimo 1029 papelitos. Con esta cota inferior, dirigimos la conversación de aula a utilizar diferentes estrategias para buscar una mejor estimación. En el artículo que os he citado al principio, se desarrollan 4 tipos de estimadores, pero en clase con los alumnos lo más razonable es que surjan los dos que planteamos a continuación.
Una de las que los alumnos acostumbran a proponer es hacer la media de los resultados extraídos.
1. La media de los resultados
Anotamos los números de los 10 papelitos que hemos sacado. Una de las conclusiones a las que llegaremos es que la media de los valores de la muestra debe ser similar a la media de todos los papelitos de la bolsa. Con los papelitos aleatorios que he sacado…
Calculamos la media y estimamos, a partir de ahí, la cantidad de papeles totales.
Podemos suponer, para una buena estimación, que si la media es m, van a quedar m-1 valores por debajo y m-1 valores por encima de la media. Así tendríamos un estimador del número total de papeles:
En nuestro caso, si calculamos la media:
Nos sale una estimación de 1123 papeles.
En este caso no nos ha pasado, pero usando este estimador, el resultado puede ser más pequeño que el mayor valor de la muestra. De hecho, al probarlo en clase, se darían cuenta.
A partir de aquí introducimos un segundo estimador, calcular la media de las distancias de las extracciones, que es el que realmente se utilizó para resolver el problema.
2. La media de las distancias
Anotamos, de nuevo, los números que hemos sacado y añadimos el 1, ya que así tendremos una distancia más sin tener que “capturar otro tanque”. Y así tenemos 10 distancias, que siempre va mejor dividir entre 10 ;p
Guiamos la conversación de aula para que se den cuenta de que una posible manera de estimar la distancia entre X10 y N puede ser encontrar la media de las distancias entre valores consecutivos de la muestra y sumarle esta “distancia media” al último valor que hemos encontrado. De esta manera, para estimar N, podemos calcular:
Hacemos notar que muchos de los números se cancelan. Como se muestra en la imagen, solo debemos saber el tamaño de la muestra y el valor más grande.
Por lo tanto, en nuestro ejemplo queda así con los valores que hemos extraído:
Y nos sale una estimación de 1132 papelitos.
3. Otros dos estimadores y la resolución del artículo de Xavier Bardina, Sílvia Prior, Carla Rodríguez y Ferran Rosado
El artículo de investigación que os he referenciado al inicio de este post, explica y aparte de desarrollar los otros dos estimadores, también demuestra que el mejor estimador es el que acabamos de presentar de hacer la media de las distancias. Esta demostración en clase de secundaria no es necesaria hacerla.
Estiramos el problema con gestión de aula y preguntas ricas
Hasta ahora, hemos probado dos estrategias de estimación, las hemos entendido y cada una nos ha dado un resultado. Pero tenemos la duda de qué estimación se ha acercado más a la realidad. Al desconocer la muestra, reflexionaremos también sobre la confianza (intuitiva) que tenemos de los resultados y como mejorar y optimizarlos.
Por ello, haremos dos preguntas clave a los alumnos, para pensar dos cosas distintas.
¿Qué tan seguros estamos de nuestra estimación?
Podemos estar más o menos seguros, pero al estar estimando, no estaremos seguros al 100%. Por ello, es razonable pensar que la estimación siempre se podrá mejorar. Así, la pregunta realmente interesante es:
¿Cómo podemos estar más seguros?
Estas dos preguntas nos darán pie a una conversación que, seguramente, nos llevará a dos opciones posibles para estar más seguros:
Ampliando la muestra, cojamos 100 papelitos.
Repitiendo el experimento 10 veces, haciendo 10 extracciones de 10 papelitos.
Hombre, lo que siempre nos han repetido es que hay que ¡aumentar la muestra! Pero, ¡un momento! Una de las cosas que he aprendido este año sobre estadística es la importancia, a nivel matemático y didáctico, de la variabilidad. Tal y como vimos en el artículo de mi visita a Oviedo y “El Problema de los Garbanzos”, así como en el Informe GAISE (Guidelines for Assessment and Instruction in Statistics Education), la variabilidad estadística era más precisa y nos daba más información que la ampliación de la muestra, y, en cambio, esto se dejaba de lado en muchas sesiones de estadística en clase de matemáticas.
Si eso fuera tan evidente y cierto, deberíamos conseguir mejores estimaciones repitiendo el experimento en lugar de aumentar la muestra. ¡Vamos a ver qué pasa!
Repitamos el experimento con estas dos estrategias para poder estar más seguros.
Ampliar la muestra
A mis 10 papelitos, le añado 90 más para poder tener una muestra de 100, aleatoria y sin reposición.
Calculamos la estimación:
Nos sale una estimación de 1116 papeles.
Repetir el experimento
Procedemos a hacer 10 extracciones aleatorias, con reposición, de 10 papelitos.
Con el mismo estimador, calculamos la estimación de cada extracción por separado y la media de las 10 extracciones:
¡Y, voilà! Con dos estrategias distintas, hemos conseguido mejorar, o al menos estar más seguros, de nuestra estimación. Mi conjetura inicial era que la estrategia de repetir el experimento, la variabilidad, me daba más información, y, por tanto, tendría que estimar mejor, que la ampliación de la muestra.
Pues, vaya liada… Parece que nuestra conjetura no se cumple… Porque os revelo que dentro de la bolsa había 1125 papelitos.
El comodín de la llamada: Luis José Rodríguez
Whatsapp directo a Luis José Rodríguez, Catedrático en Didáctica de la Matemática en la Universidad de Oviedo y experto en educación estadística y probabilidad, para exponerle mis descubrimientos. He aprendido un montón de estadística con Luis José, ¡y sigo haciéndolo!
Sobre qué estrategia para mejorar la estimación era mejor, es decir, cómo podríamos estar más seguros, fue muy interesante, y Luis José me introdujo dos conceptos que serían relevantes en la argumentación: la simetría de la distribución y el Teorema Central del Límite.
“La convergencia del TCL, si la distribución no es muy simétrica, tarda en conseguirse”. Y esto ya me dio gasolina para seguir investigando.
El Teorema Central del Límite es uno de los principios fundamentales de la estadística. Establece que, bajo ciertas condiciones, la suma (o el promedio) de un número suficientemente grande de variables aleatorias independientes e idénticamente distribuidas se aproximará a una distribución normal o gaussiana. A partir de aquí, podemos analizar la distribución y ver qué pasa.
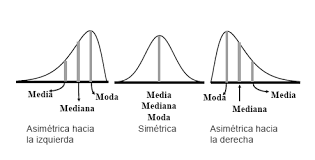
Una distribución simétrica será aquella que el lado izquierdo de la media será un espejo del lado derecho. Por ello, la media y la mediana coinciden.
Y, en nuestro caso, la distribución parece no ser simétrica. ¿Cómo podríamos saberlo con certeza?
Volvamos a nuestros tanques. ¿Qué pasa aquí?
Así que como por el TCL y al tener una distribución asimétrica, necesitamos muestras más grandes. Para llevar a cabo el experimento, he generado un simulador con sheets, para poder hacer extracciones mayores y repeticiones del experimento.
La idea es generar 100 extracciones aleatorias de 10 números entre los 1125 números correlativos que tenemos y calcular la estimación de cada grupo son los resultados de la columna I de la pestaña “SIMULADOR de 100”.
Y su media es 1132. Después ampliamos la muestra, y seleccionamos 1000 números de los 1125, y hacemos la estimación y nos da 1136.
Parece que ahora la mejor estimación es la de haber repetido el experimento, pero por muy poco y no sabemos si ha sido por “casualidad”.
Ya puestos, hice un metaexperimento: repetir 100 veces la comparativa entre hacerlo ampliando la muestra o repitiendo el experimento. Aquí, la variabilidad sí que nos dará una imagen del comportamiento de qué está pasando.
Repetimos 100 veces cada una de las opciones y comparamos cuantas veces ganaría cada opción:
Vemos que en un 81% de las veces la estrategia de ampliar la muestra se queda más cerca del número de tanques real. Corroboramos, así, lo que hemos experimentado hasta ahora en clase.
Pero que para valores de n=100, se gira la tendencia y la estrategia de repetir 100 veces el experimento va mejor que aumentar la muestra en aproximadamente ⅔ de las veces. Hay que notar que en este caso han salido 6 veces empatados.
Aunque en este problema hay otra limitación y es que podemos repetir las veces que queramos las extracciones de grupos de 10 papelitos, pero no podemos aumentar la muestra todo lo que queramos, ya que tenemos una población límite de 1125.
De hecho, recuperando nuestra conjetura de la distribución asimétrica de los resultados, gracias a la herramienta hemos podido representarlos gráficamente, en un histograma, y ver claramente como, efectivamente, los resultados no se distribuyen de forma simérica.
Curiosidad, procesos en acción y mayor aprendizaje
Recapitulemos. Hemos entendido un problema contextualizado, lo hemos manipulado, hemos reflexionado y buscado estrategias. Nos hemos hecho muchas preguntas y hemos reflexionado… ¡Esto es lo que queremos que pase en clase de matemáticas! Queremos fomentar la curiosidad, guiarla y potenciarla como docentes, para hacernos preguntas, motivar al alumnado y aprender muchas más cosas.
Y en este caso esta situación nos ha dado la oportunidad de aprender sobra la importancia de la medida de la muestra, ¡pero aún nos queda muchísimo por aprender!