Detrás de cámaras: ¿Cómo promover el razonamiento de nuestros alumnos?
Hace un tiempo, tuve la oportunidad de grabar una sesión de clase con alumnos de 1º de secundaria, donde exploraron el mundo de la probabilidad. Los profesores rara vez tenemos la oportunidad de ver clases de otros compañeros, he pensado que os puedo compartir algún trozo de la mía. ¡Hoy os llevaré detrás de cámaras! La sesión se centró específicamente en resolver un problema de probabilidad que consistía en hacer lanzamientos de monedas y avanzar por un tablero según las reglas establecidas.
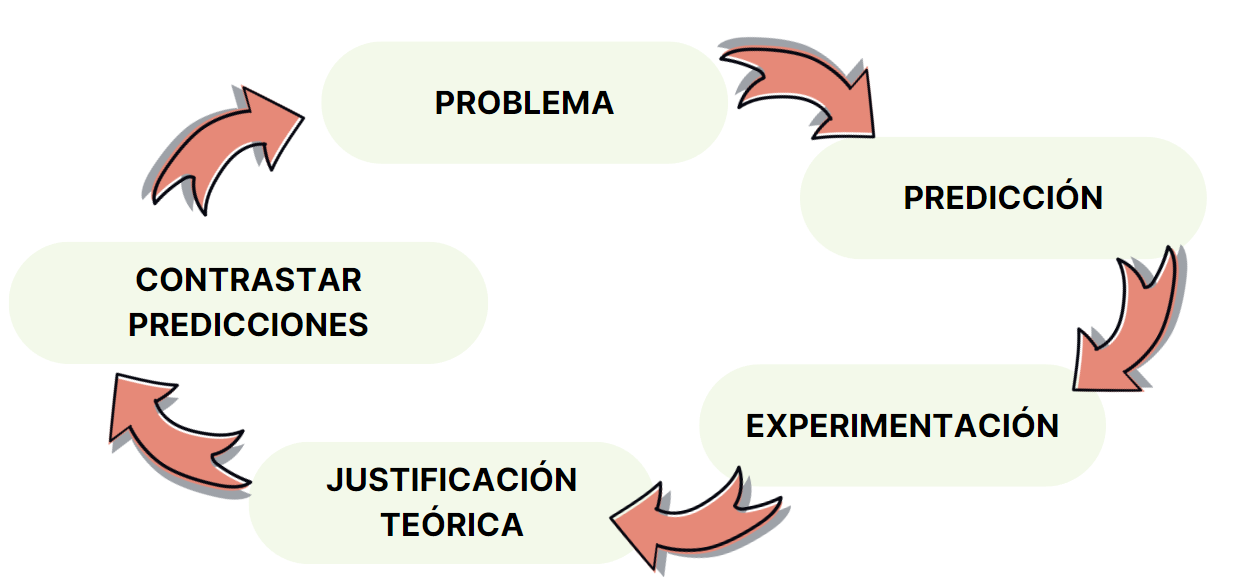
Durante las clases de probabilidad, siempre seguimos la misma estructura: primero planteamos el problema, luego hacemos predicciones, llevamos a cabo el experimento varias veces cuando es oportuno, justificamos los resultados teóricamente y finalmente contrastamos nuestras predicciones con los resultados obtenidos.
Antes de continuar, ¿queréis echarle un vistazo al enunciado? ¡Aquí lo tenéis!
Ahora os preguntaréis, ¿cómo fue la clase?
Siempre intento fomentar el razonamiento y la argumentación entre mis alumnos. Esto implica dedicar tiempo adicional a construir un "contrato didáctico", donde se enfatiza la importancia de hacer conjeturas y respaldarlas con argumentos sólidos.
Después de ver el corte de video, vemos que nos encontrábamos en pleno planteamiento del problema, analizándolo para asegurarnos de que no perdemos ningún alumno, siempre les doy algunas pistas al principio y les proporciono referencias para que puedan orientarse.
Buscamos entender qué podría suceder en el tablero, con la intención de buscar el espacio muestral. Durante el planteamiento del problema, buscamos el máximo y el mínimo de los movimientos necesarios para realizar una partida, lo cual es un subproblema que implica fomentar el razonamiento y la argumentación.
En el video, podemos ver como los alumnos sugirieron que eran necesarios 8 movimientos, ¡pero resulta que estaban equivocados! Este error nos dio la oportunidad perfecta para analizar mejor el problema y llegar juntos a la conclusión correcta: que nunca podremos ir ni a la izquierda ni hacia arriba, lo que hace imposible hacer una partida con 8 movimientos, así como también es imposible la salida por la zona azul.
Siempre evito dar la respuesta directa a los alumnos y, en su lugar, planteo preguntas abiertas que los guíen hacia las soluciones. Por ejemplo, si un alumno sugiere que el máximo son 8 movimientos, en vez de corregirlo directamente, pregunto “¿Está todo el mundo de acuerdo?”. Esto fomenta el pensamiento crítico y la participación activa, además de evitar influenciar en sus respuestas. Es importante ser ágil para no dejar que se alargue demasiado y se desvíe del tema principal.
Durante la clase, promuevo la conexión entre conceptos. Por ejemplo, un alumno sugiere una ruta en forma de “L” en 4 pasos para alcanzar la meta, de repente, otro alumno hace una conexión, ya que piensa en una simetría y sugiere otra ruta similar. Esto promueve el trabajo del proceso de comunicación y permite que construyan conocimiento conjuntamente a través de la conversación matemática.
Así, en la clase los alumnos fueron capaces de construir el conocimiento por sí mismos, sin recibir la respuesta directa, fomentando el razonamiento, la argumentación y la conexión de conceptos. Podéis ver que yo era la que dinamizaba la gestión de aula, de alguna forma, podríamos decir que la clase era magistral, pero hay que ir con cuidado de no confundirla con transmisiva.
Si te has quedado con ganas de más, ¡no te preocupes! Estoy trabajando en una serie de análisis más detallados para compartir con vosotros próximamente. Estad atentos para descubrir más sobre esta fascinante experiencia de aprendizaje. ¡No os lo perdáis!
Este análisis forma parte de una clase real que analice en una formación en directo con Cecilia Calvo en Innovamat. Podéis recuperar todas las grabaciones en YouTube.